Symmetric-Axis Transform

[manuscript as html, pdf] Implementation of the symmetric-axis transform.

[pdf manuscript] Implementation of the wave-propagation process only

[link] Using sym-axes to analyse saccadic target selection

The symmetric-axis transform takes a visual structure as input and generates symmetric-axis segments (sym-axis) as output, which express the relation between adjacent or surrounding contours. The transform was originally suggested by Blum (Blum 1967; Blum 1973). The symmetric-axis transform can be simply evolved by firstly letting the contours propagate as a wave across the image plane (see more detailed examples of wave-propagation here):

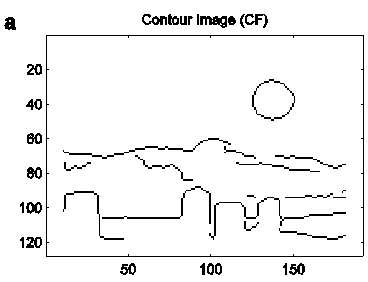
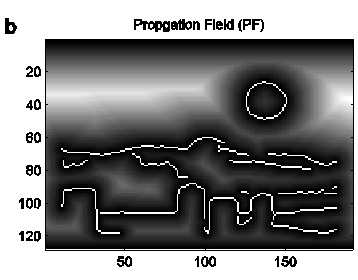
The output of the wave-propagation process is then convolved with a negative-peaked high-pass filter:

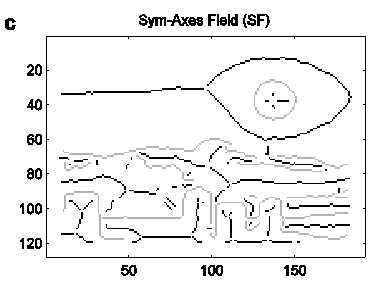
The wave-propagation process occurs in a single sweep and the entire transform can therefore be evolved quickly and in a translation-independent manner. The temporal signature of the resulting symmetric-axis segments can be easily parameterized to generate shape abstractions and the obtained parameters can explain most parallel pop-out variances as observed in visual search studies.

The symmetric-axis can be use in various ways:

1) For representation [manuscript as html, pdf]

2) To determine the fixation location within a structure [link]

3) To explain the parallel pop-out phenomena: [link]