Explaining the Pop-Out Variances as

Observed in the Study by Treisman and Gormican 1988

The following is a summary of how the decomposition output can explain the variances observed in the visual search studied by Treisman and Gormican (1988). It is emphasized, that we solely interpret the ‘variances’; it is not meant to support the feature-integration theory derived by Treisman. In contrary, our goal is to argue that these pop-out phenomena evidence a parametric structural analysis, which is based on dynamic processes and not on feature template detection.

The geometric contour parameters are called orientation, length, degree of curvature (b), degree of inflexion (t), edginess (e), wiggliness (w) and degree of isolation (r):

c(o, l, b, t, e, w, r).

The geometric sym-axis (area) parameters are initial and end distance (s₁ and s₂), angle (α), average distance (s_m), elongation (e), flexion distance and flexion location (s_fx, p_fx), curvature and orientation:

a(s₁, s₂, α, s_m, e, s_fx, p_fx, b, o).

Note: For a typical search display the SAT will not only generate sym-axes describing the local configuration of structure, but also sym-axes describing the area between elements. But because in a typical search task the subject is asked to focus on the local elements only, those ‘between-feature’ sym-axis segments are neglected. Thus, the following explanations consider local structure only.

The following figure numbers refer to the figure numbers in their seminal paper (1988).

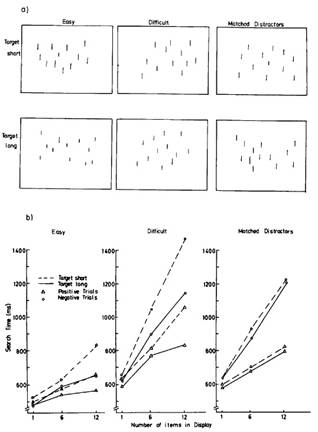
Figure 2: a deviation in the length dimension l of the contour descriptors.

Figure 3: presence/absence of a symmetric axis.

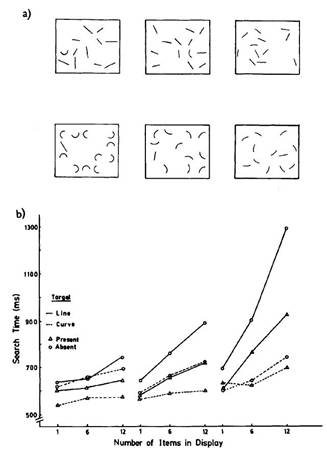
Figure 5: a deviation in the bendness dimension b of the contour vector.

Figure 6: a deviation in the orientation dimension o of the contour vector.

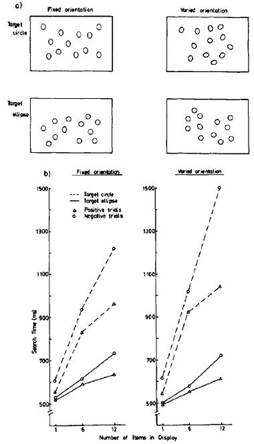
Figure 7: a deviation in the elongation dimension of the sym-axis vector (e=0 for circles); there is also a deviation in contour lengths, because a circle consists of a long, single contour, whereas an ellipse consists of two shorter contours (after segregation).

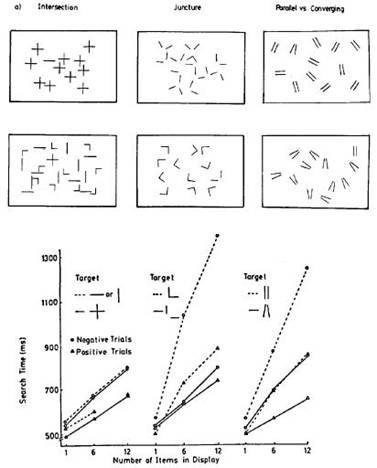
Figure 10:

- Intersection: can be explained by the absence and presence of a group of sym-axis segments whose starting points (s₁) are proximal, but such grouping has not been modeled in this study.

- Juncture: this can be interpreted as the presence or absence of a deflection, that is a deviation of the dimensions s_fx and p_fx of the sym-axis vector from their default values (center point).

- Parallel vs. Converging: a deviation of the sym-axis dimensions s₁ and s₂ or simply of the angle α.

Figure 11:

- ½: presence and absence of a sym-axis.

- ¼ and 1/8: presence or absence of a sym-axis; or a deviation in contour length.

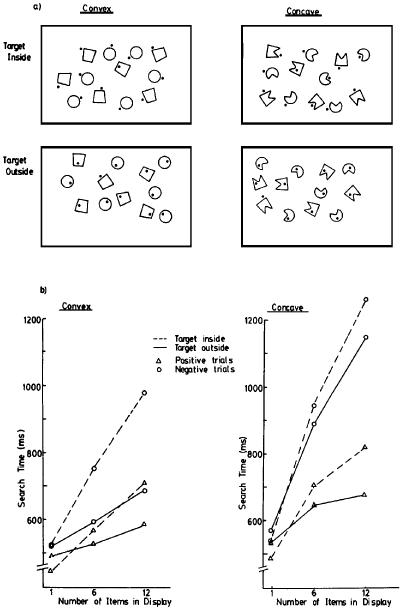
Figure 12: A deviation in the context of a sym-axis (presence/absence of neighboring sym-axes):

A point outside and near a shape generates a sym-axis which is relatively isolated as opposed to a sym-axis generated by a point inside, that is connected to sym-axes describing the entire shape. Contextual information has not been modeled yet explicitly in our models.

Discriminating parallel/serial

The distinction between parallel and serial appears to have three reasons:

1) A varying degree in the deviation, e.g. figure 5.

2) Two dimensions are different in the same visual display, e.g. finding a circle amongst ellipses of different orientations (upper right, figure 7).

3) A deviation of one dimension to one side of the scale, for instance it seems easier to find a larger distance e₂ than a smaller one, e.g. figure 10, parallel vs. converging.

The distinction between serial and parallel is not particularly considered in the following implementation and categorization analysis, as we do not aim at an emulation of saliency but rather at an exploration of the issue of representation.