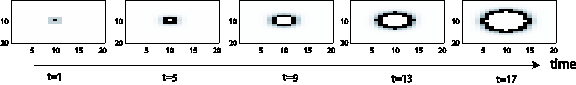Describing Structure with Symmetric-Axis
Signatures
C. Rasche
Institut für
Psychologie
Justus-Liebig
Universität
Otto-Behagel-Str
10, F1
D-35394 Giessen, Germany
Abstract
How structure is possibly represented by the visual system is still little understood. A promising concept is the symmetric-axis transform, which has already been implemented for the purpose of shape identification. However, no instantiation of this transform has been provided yet, that generates the symmetric axes for open contours. This can be achieved by the use of a wave-propagation process, whose temporal evolvement is then high-pass filtered to extract the symmetric axes. The wave-propagation process occurs in a single sweep and the entire transform can therefore be evolved quickly and in a translation-independent manner. The temporal signature of the resulting symmetric-axis segments can be easily parameterized to generate shape abstractions and the obtained parameters can explain most parallel pop-out variances as observed in visual search studies. The decomposition output was evaluated on two image collections and yielded similar performance for both collections, demonstrating the robustness of the approach. All these aspects make the decomposition process appealing as part of a biological model of structural analysis.
Introduction
The symmetric-axis transform takes a visual structure as input and generates symmetric-axis segments (sym-axis) as output, which express the relation between adjacent or surrounding contours. The transform was originally suggested by Blum (Blum 1967; Blum 1973) and has since been associated with processes of saccadic target selection (Richards and Kaufman 1969; Melcher and Kowler 1999), biological motion processing (Kovacs, Feher et al. 1998) and global-to-local processing (Kovacs and Julesz 1993). The attempts to confirm the existence of the symmetric-axis transform in the visual system have been sparse but persistent over the decades (Psotka 1978; Kovács and Julesz 1993; Burbeck and Pizer 1995; Lee, Mumford et al. 1998; Rasche 2005). The transform can in principal be implemented by a grass-fire process which evolves the symmetric axes (sym-axes) dynamically as originally suggested by Blum. However, early implementations of this transform have used a discrete propagation process which coped with the problem that multiple sym-axis segments were generated when contours were slightly deformed. Subsequent implementations have advanced the methodology by using repetitive propagation, see (Zhu 1999) for a review [Variants of this transform have also been called the medial-axis transform, if the symmetric axis was evolved from the center of a contour, e.g. (Niethammer, Betelu et al. 2004)]. Recently, Feldman and Singh have provided an improved implementation exploiting the Bayesian principle (Feldman and Singh 2006). Yet, all these implementations operate on closed shapes only, require several iterations to evolve the axes and can not deal with fragmented contour images. Furthermore, no detailed algorithm was given on how the generated sym-axes can be exploited for shape abstraction and representation.
In this study, an implementation is presented, which evolves the sym-axes using a wave-propagation process akin to the existence of traveling waves as observed in the retina for instance (Jacobs and Werblin 1998). The wave-propagation process allows generating the sym-axes for fragmented contour images and the resulting sym-axis segments can be easily employed for representation by parameterizing them. We thereby pursue a parameterization which covers a large range of geometries and which can explain the majority of parallel pop-out phenomena as determined in the visual search studies by Treisman and Gormican. (Treisman and Gormican 1988). To demonstrate the representative potential of those sym-axes, a basic-level categorization task is simulated with the images of the Corel and Caltech 101 collection.
The Model
Wave propagation
The traveling-wave process consists of a passive, sub-threshold propagation process and a spiking mechanism, which ensures active (continuous) wave propagation. This can be emulated by a (single) layer of interconnected integrate-and-fire neurons, whose spike mechanism includes a refractory period to ensure forward propagation (Koch 1999; Rasche 2007). Figure 1 shows the traveling wave for a single-pixel source, which triggers a radially outward-growing circle, like a drop on a water surface.
This temporal evolvement represents the crucial information to be held for the purpose of extracting the sym-axes: for a single point the completed evolvement can be thought of an amphitheater (circular-shaped arena): for an isolated straight contour segment the propagation looks like a coliseum or stadium (oval-shaped arena); for a rectangle, the inward propagating contours describe a roof shape; for a circle they describe a cone (see also supplementary information, figures 1 to 4). The completed temporal evolvement is now called the propagation field PF(x,y) and is a scalar 2D map. For complex scenes, the propagation field can be thought of a landscape, in which the contours run like rivers through the valley bottom, and the ridges of the hills correspond to the sym-axes as envisioned by Blum (Blum 1967; Blum 1973). An example is shown in figure 2b: bright areas denote the center of regions (high PF value=high luminance value). The sym-axes can already been recognized as ‘veins’ running through the regions.
Extracting the symmetric axes
Because a propagation field contains no ‘plateaus’ (regions of equal value), one can extract the sym-axes by convolving (*) the propagation field with a high-pass filter Fhigh emphasizing the veins, whose output is then thresholded by the function θ to obtain the symmetric field SF(x,y). SF is a sparse image with values equal the PF value at the points delineating the sym-axes:
![]() [1]
[1]
The optimal filter function is of conic shape - as generated by the contour of an isolated circle (a single symmetric point) -, whose amplitude corresponds to the symmetric distance.
An example of a symmetric field SF is shown in figure 2c. In that plot, SF is already segregated at points of intersections (see supplementary information, figure 5 for two more examples). The segregated segments often reflect the detailed relation between two contour segments. The relation is not precise as the wave propagation process has buffered small contour deformations or gaps, but it is detailed enough to express an enormous variety of geometries, as illustrated in figure 3. The relation is plotted as the symmetric distance s (taken from SF) against arc length l of the sym-axis segment in the image plane. This function is now called the symmetric signature. For two parallel straight lines (figure 3a), the signature describes a function, whose center part corresponds to the half distance between the two lines, which in turn is flanked by increasing ends because the waves continue to propagate and collide for a short while after the center part has been evolved. The symmetric signature for two inward-bent parallel lines describes a ‘depression’ function (figure 3b), the one for two outward-bent parallel lines an ‘elevation’ function (figure 3c). The two latter examples can also be regarded as a pass and a peak if one takes into account the surrounding values of the PF landscape. For an L feature, the signature corresponds to a straight line starting at s=0 (figure 3d). For an inward-bent L feature the signature starts slow and becomes faster towards its end (figure 3e). For an outward-bent L feature the signature increases faster and ends slow (saturating; figure 3f).
Parameterizing the symmetric-axis
segment
Because most segments correspond to
one of the canonical geometries depicted in figure 3, or are a variant of
those, the signature is therefore parameterized as follows. An initial and an
end symmetric distance is defined, s1
and s2, respectively, as
well as an average symmetric distance sm
(the mean of the distance vector). The slope of the signature, specifically the
straight line connecting its endpoints, serves as an estimate of the angle α between the two surrounding
contours. A measure of elongation e is
determined by dividing the segments arc length (l, see above) by its average symmetric distance sm, e=l/ sm,![]() ; 0=circle, 1=oval). To capture the flexing of the adjacent
contours, the inward and outward bending, the point which is maximally distant
from the straight line connecting the signature’s endpoints is determined, and
its distance value sfx and
relative location pfx within
the symmetric signature are taken (see supplementary information, figure 7). If
such a distance is absent, as in case of parallel lines, the center point is
taken. To characterize the geometry of the sym-axis, its orientation and
curvature in the image plane is determined: the orientation o is defined as the orientation of the straight
line connecting the segment’s endpoints and the curvature b as the maximal distance between the segment and the straight
line.
; 0=circle, 1=oval). To capture the flexing of the adjacent
contours, the inward and outward bending, the point which is maximally distant
from the straight line connecting the signature’s endpoints is determined, and
its distance value sfx and
relative location pfx within
the symmetric signature are taken (see supplementary information, figure 7). If
such a distance is absent, as in case of parallel lines, the center point is
taken. To characterize the geometry of the sym-axis, its orientation and
curvature in the image plane is determined: the orientation o is defined as the orientation of the straight
line connecting the segment’s endpoints and the curvature b as the maximal distance between the segment and the straight
line.
In addition to the above 9 geometric parameters, we add 6 ‘appearance’ parameters, which characterize the luminance distribution of the area as outlined by the signature using simplest statistics: For the distribution of luminance values, the mean, standard deviation and range are determined, cm, cs and cr. These parameters are also determined after the image was processed with a blob filter to capture larger, local variations in the luminance distribution, which here are called fuzziness (fm, fs, fr). In summary, we will test the following 15-dimensional vector for a sym-axis segment, also called area:
a(s1, s2, α, sm, e, sfx, pfx, b, o, cm, cs, cr, fm, fs, fr).
Relating sym-axis segments
In order to build abstractions of more complex shapes, one could analyze the full geometry of the intersecting sym-axis segments, but a first step is to analyze the surrounding PF values: a circle is placed at the intersection point with a radius corresponding to the distance value (grey circle in figure 4). The PF values along the circle’s arc-length variable k describe a signature reflecting the surrounding ‘parts’ or ‘features’. For a circle shape, this surround signature is flat because the values are taken along the contour where the PF values are 0 (figure 4a). For a square shape, the signature shows 4 elevations which correspond to the crossing of the sym-axis segments (the diagonals; figure 4b). For the intersection of sym-axes of a rectangle, there are only three elevations, with the largest one corresponding to the central axis segment reflecting the rectangle’s longitude (figure 4c). For an open rectangle, this large amplitude even exceeds the symmetric distance of the intersection point thus indicating the large openness of the surrounding structure. The surround signature allows to easily estimate the openness u of the intersecting sym-axis segment by dividing the signature’s integral by its diameter: u=1/(2 sc )∫PF(k) (0=circle; 1=open rectangle for instance). To further specify the geometry we determine the number n of elevations, the amplitude β for each elevation and the angle α between the locations of the amplitude maxima. For the list of amplitudes and angle values, we take the standard deviation, σβ and σα , respectively. The three largest amplitude and angle values were also selected as dimensions (β1, β 2, β 3 and α1, α2, α3), thus forming an 11-dimensional intersection vector i:
i(sc, u, n, σβ,
σα, β1,
β 2, β 3, α1, α2,
α3).
To express complex shapes more elaborately, we form a skeleton vector k with simple statistics taken from the geometrical parameters of the intersecting segments. The parameterization can be regarded as an elaboration to the intersection vector:
k(sc,
n, a, smin, smax, lmin, lmax, lmean,
lstd, αmin, αmax, cm, cs,
cr, fm, fs, fr).
Dimension sc is the symmetric distance value at the point of intersection; dimension n is the number of intersecting segments; dimension a is the spatial (2D) area of the entire structure; dimensions smin and smax are the minimal and maximal distance value for the distal (outer) ends of the intersecting segments; analogously, dimensions lmin and lmax are the minimal and maximal length of the segments; dimensions lstd and lmean are the standard deviation and mean of the length values. In addition to those 11 geometric parameters, the same luminance and fuzziness parameters are added as for the area vector (cm, cs, cr, fm, fs, fr), taken from the area spanned by the intersecting segments, thus forming the above 17-dimensional vector.
Explaining
parallel pop-out variances
The decomposition has provided a number of parameters, which can explain all the pop-out phenomena as observed in the visual search study by Treisman and Gormican for instance (Treisman and Gormican 1988) – except of those involving isolated contour segments such as the orientation and curvature pop-out. Modeling studies mimicking visual search have attempted to explain these variances, but can do so only to a limited extent, e.g. (Itti and Koch 2001; Li 2002), thereby following the idea of feature detection (Treisman 1988). In contrast, the present decomposition generates the relations between contours dynamically and not as the result of template matching. The decomposition generates an output from which the variance can be read out as parameter differences: pop-out can therefore be determined as the variance in a multi-dimensional space.
For a typical search display, the decomposition will not only generate sym-axes describing the local configuration of structure, but also sym-axes describing the area between structural elements. The results of the visual search study by Treisman and Gormican are therefore explained considering local structure only. The presence or absence of a pair of lines may be explained by the presence or absence of a (local) sym-axis. The circle-vs.-ellipse pop-out can be explained by a deviation in the elongation dimension e of the area vector (e=0 for circles, e>0 for ellipses). The parallel-vs.-converging pop-out results from a difference in the angle α of the area vector. The presence or absence of a juncture is a deviation in the flexion parameters (distance value sfx and relative location pfx). The circle-vs.-arc pop-out can also be explained by either the presence or absence of a sym-axis, whereby the arc is a half circle or a circle with a ¼ or 1/8 gap.
The following two kinds of pop-out can be explained by a local grouping of sym-axes. The absence or presence of a cross-intersection – which generates four small sym-axes - can be explained by the absence and presence of a group of sym-axis segments whose starting points (s1) are proximal. The adjacent-point pop-out (figure 12 in Treisman and Gormican) can be explained by the contextual analysis of the sym-axes: A point outside and near a shape generates a sym-axis, similar to the one in figure 3b, which is isolated as opposed to a sym-axis generated by a point inside, that is ring-connected to the sym-axes describing the entire shape. Such grouping has not been modeled yet in this study, although it could potentially contribute to better categorization performance.
Methods
The full Corel collection (60000 images) provides 100 image classes, of which 357 belong to a human subordinate category. These were pooled into 112 basic-level categories (Rosch, Mervis et al. 1976; Oliva and Torralba 2001). Examples of basic-level categories are wild animals (27, 4.5%) [number of image classes, proportion of the entire collection], patterns (25,4.2%), sports (25, 4.2%), flowers (17, 2.8%), aircrafts (16, 2.7%), models (13, 2.2%), birds (11, 1.8%), water animals (10, 1.7%), cars (9, 1.5%), canyons (7, 1.2%), different cultures (7, 1.2%), mountain sceneries (7, 1.2%), ships (7, 1.2%). The complete list of category labels is accessible at http://www.allpsych.uni-giessen.de/rasche/research/res_COREL_cat.htm.
The subsample size was 10 images
per category for the Caltech collection (1010 images per entire subsample) and
10% images per category for the Corel collection (typically 10 or 20 images;
3570 images per entire subsample), for both the learning and testing procedure.
The images for a subsample were selected randomly and categorization
performance was tested with 3 different subsamples using cross validation.
The images of the Corel draw collection were downsampled to a size of 128 x 192 pixels. This low resolution was chosen intentionally to force the search of useful area parameterization – humans can easily recognize these low-resolution images. Most images of the Caltech collection are at a resolution of approximately 200x300 and were not changed in size, but larger images were downsampled to that size.
To extract contours, the gray-scale image I was processed with the Canny algorithm at fine/coarse scales (σ) equal 1, 2, 3 and 5 (Canny 1986). The starting point of propagation (t=0) is the contour image: PFt=0(x,y)=CF(x,y). Propagation is emulated by repeatedly convolving PFt with a 2D Gaussian-shaped low-pass filter g(i,j) (3x3 matrix, std dev = 0.5): PFt+1(x,y) = PFt(x,y)*g(i,j). After each time step PFt is thresholded by setting those matrix elements to 1, which have a value larger than a fixed threshold θprop, the other values remain: PFt=1, for all PFt > θprop, else PFt = PFt (θprop=0.12). The final propagation matrix, PFt=final(x,y), is then simply called PF (see also supplementary information, figures 1 to 5). The high-pass filter Fhigh to compute the symmetric field SF is a (fixed-size) DOG with standard deviations of 0.833 and 1.5. This crude filter approximation is made for reason of simplicity, because the use of the optimal, distance-dependent filter is computationally much more expensive.
To compute the luminance statistics (cm, cs, cr), I was processed with a local filter determining range, mean and standard deviation, Irng, Imean and Istd. The filter size was 5x5 pixels for scales 1 and 2, 7x7 pixels for scale 3 and 9x9 pixels for scale 5. To obtain the fuzziness values (fm, fs, fr), I was processed with 2 DOG filters of different size, a 3x3 pixel size with standard deviations of 0.5 and 1.0; and a 5x5 pixel size with standard deviations of 1.0 and 2.0. The output of both image convolutions is summed to a single image from which fm and fs are determined for the area and skeleton descriptor (a and k) on each scale.
Results
A summary of the decomposition output is shown in figure 5. The red dot marks the location of s2, which is the open side in case of converging lines or an L feature. The red circle marks the location of pfx. As the structure of a gray-scale image is typically ‘smeared’, especially in case of natural scenes, the resulting contour images are fragmented. For that reason, some of the regions outlined by the skeleton descriptor k (3 or more intersecting sym-axis segments) are accidental and do not always correspond to the interpreted regions. The issue is similar to the issue of contour extraction, but addressing this is beyond the scope of a single study. The aim of the present study is to introduce a model of the symmetric-axis transform and to proof its potential by a simple categorization task.
The categorization test was performed using the images of two different image collections, the Caltech 101 and the Corel collection. The images of the Caltech collection contain 101 categories showing exclusively single objects with relatively clear silhouettes and limited geometric variability (Li, Fergus et al. 2006). To test also complex scenes - containing multiple objects and ‘smeared’ object contours -, the images of the Corel collection were used, which were ordered into 112 basic-level categories. Many categories show large geometric variability and overlapping representations. To test the usefulness of proposed parameters, a categorization task using a histogramming approach was tested first. To demonstrate the specificity of the individual descriptors, image sorting was carried out.
Histogramming
For the list of descriptors (a, i or k) for a given image, a 10-bin histogram for each dimension is constructed. The histograms are then concatenated to form a 430-dimensional image vector. The performance for correct categorization was between 9.8 and 12 percent for all 4 scales for both collections (figure 6a and b, labeled ‘F’). Omitting the distracter category (‘Google’ images in Caltech collection) decreased the performance by 0.3 percent only. To estimate the contribution of the individual descriptors and its dimensions, the performance was also determined when only a subset of dimensions was used. When using only the area parameters (150-dimensional image vector), the performance decreased to a value of 8 to 10.5 percent, see label ‘a’. For the geometrical parameters of the area descriptor (90-dimensional vector), the performance decreased little for the Caltech collection but rather dropped for the Corel collection (down to ca. 5 percent, see label ‘a-geo’), which exposes the characteristic, that the Caltech collection contains objects with limited geometric variability. When only the appearance parameters were employed (label ‘a-app’), the performance decreased slightly more for the Caltech collection but even increased for the Corel collection. This reveals that the strongest cue for the categorization performance is the appearance and is slightly stronger in the Corel collection. A similar performance pattern can be observed for the skeleton descriptors (‘k’, ‘k-geo’, ‘k-app’). The intersection descriptor, which represents geometry only, yielded a performance of 4 to 5 percent (‘i’). Two combinations of descriptor were tested, areas and intersections (‘a&i’), as well as areas and skeletons (‘a&k’), whose performance barely exceeds the performance of the area descriptors along (‘a’). Hence, the different descriptors do not add up in the histogramming approach and the categorization percentage of ca. 12 percent appears to be an upper limit.
To estimate the significance of individual dimensions, the categorization performance was tested when single dimensions were knocked out (420-dimensional vector, figure 7). The performance decreased only slightly (ca. 0.3 percent), which demonstrates that none of the dimensions is crucially more significant than any other one - an analysis of the covariance of the dimension values did not show any strong dependencies either. The performance decrease merely indicates preferences, for instance for the orientation and bendness dimension of the area descriptor (no. 1 and 9, figure 7) contribute more to category distinctness than for instance the range of luminance values and the standard deviation of the fuzziness dimensions (no. 12 and 14).
Figure 6c shows the performance across scales, showing there is only a small dependence of the histogramming method on the exact scale. Figure 6d demonstrates that even for a smaller number of learning samples (2 and 5 images) reasonable performance can be achieved.
Descriptor Matching
In a learning phase, category-specific descriptors (a, i or k) were searched for each category. A selected descriptor (e.g. the L-feature of a chair) was compared to all other descriptors of the remaining images and the distances sorted by decreasing similarity. The category-specificity of a descriptor was defined as the percentage of images belonging to the same category (chair) for the first 100 images of the corresponding first 100 similar descriptors was taken. Only descriptors with a minimum specificity of 2 percent were kept (figure 8). The category specificity could reach up to tens of percent and was 3.5 to 8 percent in average: for the Caltech collection the average was 7.5 percent for the area and skeleton descriptors, and 4.5 percent for the intersection descriptors; for the Corel collection the average percentage was lower by ca 1.0 for each descriptor. Differences across scales were small (ca. 1 percent).
In a testing phase, the list of collected category-specific descriptors were matched against the images of another subsample. For each image, the descriptors vj were matched against the collected descriptors vi of each category, resulting in a distance matrix Dij. The shortest distance for each collected descriptor was selected di=maxjDij. This distance vector reflects the optimal match between a selected image and a category representation. The distance vector di was sorted and the first 2, 5 and 10 differences summed (d∑2, d∑5, d∑10), followed by determining the category-specificity for each ‘integral’. A systematic search was carried out for the maximal ‘integral’ value across all descriptors for 3 different scales (2, 3 and 5). The maximal value was in average 22 percent for the Corel collection and 28 percent for the Caltech collection, demonstrating the high distinctness of the vectors. The performance difference for the two collections can again be explained by the differing degree of structural variability of categories within the two image collections. However, we were not capable yet, to exploit this descriptor specificity to achieve a categorization performance, which exceeds the performance of the histogramming approach.
For both types of analyses, histogramming and descriptor matching, the radial-basis function was employed as distance measure. Using the Euclidean distance function did not change performance significantly. A number of different, exact definitions for some of the dimensions were tested, as well as alternate dimensions for the intersection and skeleton parameters. All these variations did not alter overall performance significantly, suggesting that the decomposition is of general nature and not biased toward a specific set of images.
Discussion
The purpose of the evaluation was to demonstrate the potential of the present implementation of the symmetric-axis transform, not to argue for a specific model of the categorization process or of basic-level representation. The model is neither considered a complete model of structural description. A complete description required also the parameterization of contours – as evidenced by the parallel pop-out phenomena such as curvature discrimination. One important property of our model is that it allows determining the area of open regions as contour images are always fragmented. Especially natural scenes often have little specific structural geometry and are better described by their characteristic textures of those regions (figure 5).
The chosen geometric parameters describe commonly occurring simple structures (figure 3) and suffice to explain all parallel pop-out variances as observed in visual search studies – with exception of the orientation and curvature pop-out, for which an explicit contour description had to be pursued. Those pop-out effects are generally interpreted as supporting the traditional viewpoint of recognition evolvement, namely that of a gradual local-to-global integration along a hierarchy spanning several visual areas (Hubel and Wiesel 1968; Barlow 1972; Essen, Felleman et al. 1990). But a newer viewpoint is that some form of global integration already takes place in early visual cortical areas using for instance horizontal connections amongst cells of the same neocortical layer, thus arguing rather for a global-to-local recognition evolvement, e.g. (Kovacs 1996; Li 1998; Pettet, McKee et al. 1998; Hess and Field 1999; Rasche and Koch 2002). Some of those studies have suggested that processes like the symmetric-axis transform occur. We now have provided a biologically plausible implementation of it, whose output can explain most parallel pop-out phenomena. Thus, the symmetric-axis transform provides a convenient way to transform any structure. However it does not follow any hard-wired integration schemes: it is its wave-propagation process, that allows to flexibly evolve a temporal landscape, the propagation field, from which the parameters can be easily extracted. To clarify our point, the fact that one can explain most of the parallel pop-out phenomena with a parameterization of the propagation field does not support any specific theory on the issue of parallel or serial processing. Rather, it can be regarded as a strong argument that processes such as the symmetric-axis transform and the presented parameterization, are likely to occur in the visual system. It rather seems to us, that the pop-out phenomena express a systematic parameterization of structure not a feature search.
The choice of parameters for the skeleton and the intersection vectors was an intuitive one. But modifications of the parameters did not alter the results significantly. The reason is that the basic-level categorization task is a rather ‘coarse’ type of classification. The issue is of such a high complexity, that it is a priori not clear, which parameters may actually be crucial or sufficient for a discrimination between all categories. If an identification task was pursued, then the exact definitions may matter and a higher number of parameters may be necessary to properly describe and distinguish the objects.
The transform sketches an alternative approach to the issue of translation independence, which so far has been exclusively modeled in a hierarchical fashion (Riesenhuber and Poggio 1999; VanRullen and Thorpe 2002). The hierarchical approach is limited by its own pyramidal architecture and to escape this bottleneck, models are sometimes additionally equipped with a simulation of attentional shifts (Amit and Mascaro 2003). Whether such attentional shifts occur during categorization is still being debated (Li, VanRullen et al. 2002), but more recent experiments (Kirchner and Thorpe 2006) strongly challenge that view and encourage to find alternate models.
The translation independence here is achieved by a wave-propagation process. Such processes do occur in visual systems at the retinal and cortical level (Grinvald, Lieke et al. 1994; Bringuier, Fregnac et al. 1997; Senseman 1999; Prechtl, Bullock et al. 2000).
The question is whether such waves can occur also quickly enough to support fast categorization, see (Barch and Glaser 2002; Rasche 2005) for supporting arguments on the neurophysiological level. But because the transform can be evolved in a single ‘sweep’ it could potentially take place within 150ms, the average duration it takes to categorize a canonical image (Palmer, Rosch et al. 1981; Thorpe, Fize et al. 1996).
The transform may also serve as a substrate for saccadic target selection, a process which occurs at a similar speed. For instance, saccades made toward shapes land in preferred locations and those locations were associated with the symmetric axis transform (Kaufman and Richards 1969; Richards and Kaufman 1969). Such locations can only be computed if there is an explicit representation of region as for instance given by the symmetric-axis signatures. A study by Melcher and Kowler proposed that rather the center-of-area is used for saccadic target selection (Melcher and Kowler 1999), but the computation of that center could also be carried using the symmetric axis.
The performance for the Caltech collection does not nearly reach the performance of current state-of-the art computer vision methodology, which obtain more than 90 percent correct categorization on the Caltech database using data-clustering methodology such as principal component analysis (Fergus, Perona et al. 2007). That methodology works exceptionally well on objects depicted in gray-scale images with limited geometrical variability and relatively clear contours, but an extension to noisier images and categories with overlapping representations remains to be elaborated. For that purpose we also tested low-resolution images (128x192 pixels) of the Corel collection, which contains categories of large geometric variability, and for which a comparable performance was obtained.
The performance of the intersection vector - containing mere geometric information -, almost reached the performance of the skeleton vector when the latter was tested with the geometric parameters only (compare ‘i’ and ‘k-geo’ in figure 6). This indicates that the intersection vector, whose geometrical information was solely taken from the circular surround (figure 4), represents already a useful abstraction of complex shapes, and that some form of classification can be done using the propagation field only, without requiring the explicit analysis of sym-axes segments.
There are many possibilities to improve the performance of the present approach – apart from including a contour description.
1) It may just require the appropriate learning algorithm, which determines category-specific combinations of descriptors. So far only descriptor combinations of the same type have been tested (the ‘integral’), for which we already achieved a specificity of more than 20 percent for each collection.
2) Performance could also be increased by grouping descriptors, such as the grouping of proximal starting points (s1) of sym-axes segments to form contour intersections.
3) Scale selection may also improve performance, but the analysis of category-specific descriptors (figure 8; see supplementary material figure 7 for category-specific descriptors for all categories for two scales) shows that for some categories the category-specific structural information differs between the fine and the coarse scale. Hence, a representation consisting of descriptors from different scales should also be considered and not only a selection of a specific scale.
4) The choice of appearance dimensions is rather simple (luminance and fuzziness dimensions; cm, fm,…): texture perception studies have shown that the detailed distribution of luminance values seems to be a strong determinant for proper texture identification (Dror, Willsky et al. 2004; Motoyoshi, Nishida et al. 2007). A more thorough parameterization of the luminance distribution may therefore be appropriate.
Despite the elimination of one or a few dimensions, categorization performance dropped only slightly (figures 5 and 6). This may explain why humans can recognize rotated pictures equally rapid as non-rotated (up-right) pictures (Guyonneau, Kirchner et al. 2006): the presence of the remaining unaltered aspects may still allow for this rapid categorization. Nevertheless we hypothesize that eliminating dimensions will lead to prolonged categorization durations. Such a prolongation may be difficult to measure if only a single dimension is eliminated and if only a small data set is collected. We predict that with an increase in the number of eliminated dimensions, the categorization duration gradually prolongs, which could also be measured with data sets of regular size. The elimination of dimensions can be carried out by image modifications using computer vision methodology.
Acknowledgements
CR is supported by the Gaze-based Communication Project (contract no. IST-C-033816, European Commission within the Information Society Technologies). CR would like to thank Karl Gegenfurtner for support.
References
Amit, Y. and M. Mascaro (2003). "An integrated network for invariant visual detection and recognition." Vision Research 43(19): 2073--2088.
Barch, D. and D. A. Glaser (2002). "Slowly moving stimuli induce characteristic periodic activity waves in an excitable membrane model of visual motion processing." NEUROCOMPUTING 44: 43-50.
Barlow, H. B. (1972). "Single units and sensation: a neuron doctrine for perceptual psychology?" Perception. 1(4): 371-94.
Blum, H. (1967). "A New Model Of Global Brain Function." Perspectives In Biology And Medicine 10(3): 381--\&.
Blum, H. (1973). "Biological Shape And Visual Science .1." Journal Of Theoretical Biology 38(2): 205--287.
Bringuier, V., Y. Fregnac, et al. (1997). "Synaptic origin and stimulus dependency of neuronal oscillatory activity in the primary visual cortex of the cat." J Physiol (Lond) 500 ( Pt 3): 751-74.
Burbeck, C. A. and S. M. Pizer (1995). "Object Representation by Cores - Identifying and Representing Primitive Spatial Regions." Vision Res. 35(13): 1917-1930.
Canny, J. (1986). "A COMPUTATIONAL APPROACH TO EDGE-DETECTION." IEEE Transactions on Pattern Analysis and Machine Intelligence 8(6): 679--698.
Dror, R., A. S. Willsky, et al. (2004). "Statistical characterization of real-world illumination." Journal Of Vision 4(9): 821-837.
Essen, D. C. V., D. J. Felleman, et al. (1990). "Modular and hierarchical organization of extrastriate visual cortex in the macaque monkey." Cold Spring Harb Symp Quant Biol 55: 679-96.
Feldman, J. and M. Singh (2006). "Bayesian estimation of the shape skeleton." PNAS 103: 18014-18019.
Fergus, R., P. Perona, et al. (2007). "Weakly supervised scale-invariant learning of models for visual recognition." International Journal Of Computer Vision 71(3): 273--303.
Grinvald, A., E. E. Lieke, et al. (1994). "Cortical Point-Spread Function And Long-Range Lateral Interactions Revealed By Real-Time Optical Imaging Of Macaque Monkey Primary Visual-Cortex." Journal Of Neuroscience 14(5): 2545--2568.
Guyonneau, R., H. Kirchner, et al. (2006). "Animals roll around the clock: The rotation invariance of ultrarapid visual processing." Journal Of Vision 6(10): 1008--1017.
Hess, R. and D. Field (1999). "Integration of contours: new insights." Trends In Cognitive Sciences 3(12): 480--486.
Hubel, D. H. and T. N. Wiesel (1968). "Receptive fields and functional architecture of monkey striate cortex." The Journal of physiology 195(1): 215-43.
Itti, L. and C. Koch (2001). "Computational modelling of visual attention." Nature Reviews Neuroscience 2(3): 194--203.
Jacobs, A. L. and F. S. Werblin (1998). "Spatiotemporal patterns at the retinal output." JOURNAL OF NEUROPHYSIOLOGY 80(1): 447--451.
Kaufman, L. and W. Richards (1969). "Spontaneous fixation tendencies for visual forms." Perception \& Psychophysics 5: 85-88.
Kirchner, H. and S. J. Thorpe (2006). "Ultra-rapid object detection with saccadic eye movements: Visual processing speed revisited." Vision Research 46(11): 1762--1776.
Koch, C. (1999). Biophysics of Computation: Information Processing in Single Neurons, Oxford University Press.
Kovacs, I. (1996). "Gestalten of today: Early processing of visual contours and surfaces." Behavioural Brain Research 82(1): 1--11.
Kovacs, I., A. Feher, et al. (1998). "Medial-point description of shape: a representation for action coding and its psychophysical correlates." Vision Res 38(15-16): 2323-33.
Kovacs, I. and B. Julesz (1993). "A closed curve is much more than an incomplete one: effect of closure in figure-ground segmentation." Proc Natl Acad Sci U S A 90(16): 7495-7.
Kovács, I. and B. Julesz (1993). "A Closed Curve Is Much More Than An Incomplete One - Effect Of Closure In Figure Ground Segmentation." Proceedings Of The National Academy Of Sciences Of The United States Of America 90(16): 7495--7497.
Lee, T. S., D. Mumford, et al. (1998). "The role of the primary visual cortex in higher level vision." Vision Res. 38(15-16): 2429-2454.
Li, F. F., R. Fergus, et al. (2006). "One-shot learning of object categories." IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE 28(4): 594-611.
Li, F. F., R. VanRullen, et al. (2002). "Rapid natural scence categorization in the near absence of attention." Proceedings of the National Academy of Scienes of the United States of America 99: 9596-9601.
Li, Z. P. (1998). "A neural model of contour integration in the primary visual cortex." Neural Computation 10(4): 903--940.
Li, Z. P. (2002). "A saliency map in primary visual cortex." Trends In Cognitive Sciences 6(1): 9--16.
Melcher, D. and E. Kowler (1999). "Shapes, surfaces and saccades." Vision Research 39(17): 2929--2946.
Motoyoshi, I., S. Nishida, et al. (2007). "Image statistics and the perception of surface qualities." Nature 447(7141): 206-209.
Niethammer, M., S. Betelu, et al. (2004). "Area-based medial axis of planar curves." International Journal Of Computer Vision 60(3): 203-224.
Oliva, A. and A. Torralba (2001). "Modeling the shape of the scene: A holistic representation of the spatial envelope." Int. J. Comput. Vis. 42(3): 145-175.
Palmer, S. E., E. Rosch, et al. (1981). Canonical perspective and the perception of objects. Attention and performance IX. J. Long and A. Baddeley. Hillsdale, NJ, Erlbaum: 135-151.
Pettet, M. W., S. P. McKee, et al. (1998). "Constraints on long range interactions mediating contour detection." Vision research. 38(6): 865-79.
Prechtl, J. C., T. H. Bullock, et al. (2000). "Direct evidence for local oscillatory current sources and intracortical phase gradients in turtle visual cortex." Proc. Natl. Acad. Sci. U. S. A. 97(2): 877-882.
Psotka, J. (1978). "Perceptual processes that may create stick figures and balance." J. Exp. Psychol.-Hum. Percept. Perform. 4(1): 101-111.
Rasche, C. (2005). "A Neural Architecture for the Symmetric-Axis Transform." Neurocomputing 64: 301-317.
Rasche, C. (2005). "Speed Estimation with Propagation Maps." NEUROCOMPUTING 69: 1599-1607.
Rasche, C. (2007). "Neuromorphic Excitable Maps for Visual Processing." IEEE Transactions On Neural Networks 18(2): 520-529.
Rasche, C. and C. Koch (2002). "Recognizing the gist of a visual scene: possible perceptual and neural mechanisms." NEUROCOMPUTING 44: 979--984.
Richards, W. and L. Kaufman (1969). ""Center-of-gravity" tendencies for fixations and flow patterns." Perception and Psychophysics 5: 81-84.
Riesenhuber, M. and T. Poggio (1999). "Hierarchical models of object recognition in cortex." Nature Neuroscience 2(11): 1019--1025.
Rosch, E., C. B. Mervis, et al. (1976). "Basic objects in natural categories." Cognitive Psychology 8: 382-439.
Senseman, D. M. (1999). "Spatiotemporal structure of depolarization spread in cortical pyramidal cell populations evoked by diffuse retinal light flashes." Visual Neuroscience 16(1): 65--79.
Thorpe, S., D. Fize, et al. (1996). "Speed of processing in the human visual system." Nature 381: 520-522.
Treisman, A. (1988). "Features and objects: the fourteenth Bartlett memorial lecture." Q J Exp Psychol [A] 40(2): 201-37.
Treisman, A. and S. Gormican (1988). "Feature analysis in early vision: evidence from search asymmetries." Psychol Rev 95(1): 15-48.
VanRullen, R. and S. J. Thorpe (2002). "Surfing a spike wave down the ventral stream." Vision Research 42(23): 2593--2615.
Zhu, S. C. (1999). "Stochastic jump-diffusion process for computing medial axes in markov random fields." IEEE Transactions on Pattern Analysis and Machine Intelligence 21: 1158-1169.
Figure 1. Wave propagation for a single-point source. 5 snap
shots of the evolvement are shown. Gray-scale pixels: passive, sub-threshold
wave. Black pixels: spike front.
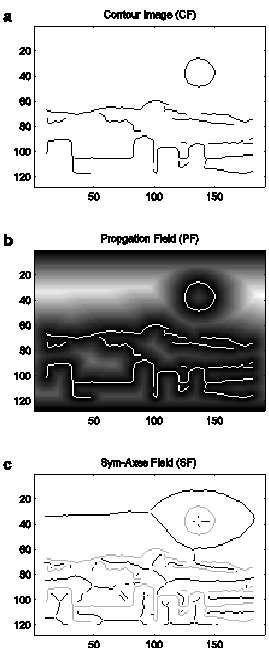
Figure 2. a.
Contour image (CF). b. Propagation
field (PF): Completion of wave propagation: increasing luminance values reflect
temporal evolvement (contours in white). The symmetric axes are already visible
as ‘veins’. c. Symmetric-axis field (SF)
in black (contours in gray). The field is already segregated into sym-axis
segments at points of intersections.
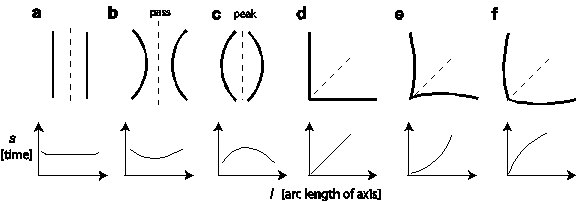
Figure 3. Symmetric-distance signatures of typical sym-axis
segments. The signature relates arc length l
of the sym-axis segment - as laid out in the image plane - with its
symmetric distance value s (or temporal
evolvement; taken from SF). a. The signature for two parallel
contour segments. b. The signature
for two inward-bent parallel contours; they form a pass if one traverses the PF map from one contour side to the
other. c. The signature of two
outward-bent parallel contours form a peak. d-f. Signature of L features with contour variation analogous to
cases in a-c.

Figure 4. Surround signature of characteristic sym-axis
intersections. The signature relates the PF values with arc-length variable of
a circle, whose radius corresponds to the symmetric distance of the
intersection point (dashed line = symmetric distance of point of intersection).
a. A circle (a single symmetric
point) results in a flat signature. b.
The intersection point of a square results in an ‘undulating’ signature. c. The intersection point for a closed
rectangle results in 3 elevations with the PF amplitude of the largest one
corresponding to the distance of the intersection point. d. The signature for an open (half) rectangle: the PF amplitude for
the open side exceeds the distance of the intersection point.
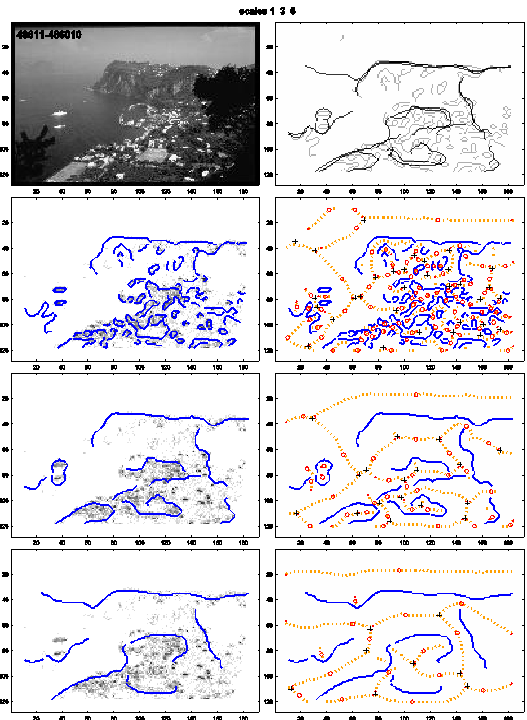
Figure 5. Summary of the decomposition (σ=1,
3 and 5). Top right: Contours of all three scales overlaid. Left column: Blue: contours; gray-scale
pixels: output of fuzziness (blob) filter. Right
column: Blue: contours; orange-dotted: sym-axes; red dot: s2; red circle: pfx; Plus sign: intersections of sym-axes.
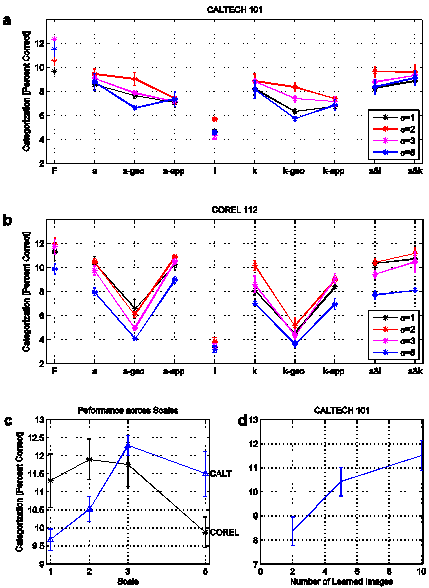
Figure 6: Categorization results of histogram matching. a, b: Correct categorization for full
‘F’ and partial dimensionality (‘a’, ‘a-geo’, ‘a-app’…) for 4 different
coarse/fine scales (σ=1, 2, 3 and 5). Error bars denote standard error of
3-fold cross validation. c: Correct
categorization performance for full dimensionality (‘F’) across coarse/fine
scale. d: Correct categorization
performance for different numbers of learned images, scale 5, full
dimensionality (Caltech collection only).
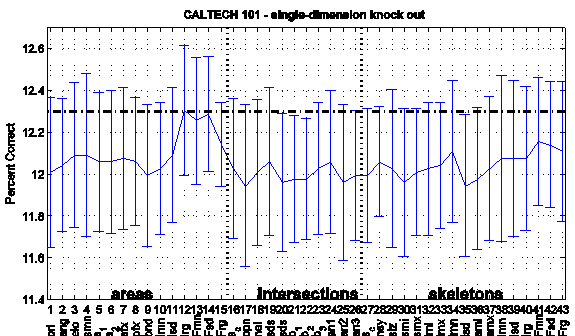
Figure 7. Categorization performance (proportion correct) for
single-dimension knock out (Caltech collection). The performance for full
dimensionality (430 dimensions) is indicated as black dashed line at ca. 12.3
percent, the blue values show the knock-out performance (420 dimensions). From
left to right: dimensions of a, i and k.
Error bars denote standard error of 3-fold cross validation.
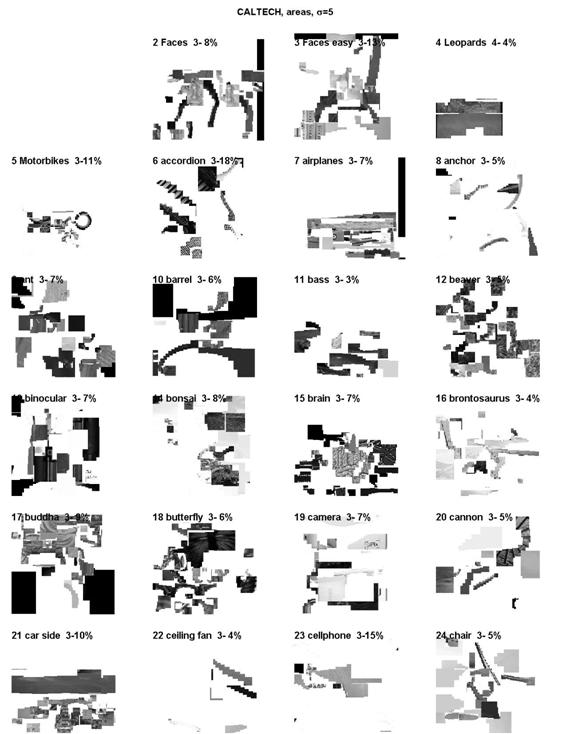
Figure 8. Category-specific sym-axis segments for
some categories of the Caltech collection (σ=5). The percentage indicates
the number of same-category images for the first 100 images containing similar
descriptors.